Startseite » Forum » beweisen das teilmenge ein untervektorraum
beweisen das teilmenge ein untervektorraum
Universität / Fachhochschule
Vektorräume
Tags: Vektorraum
 |
|---|
|
Hallöli, ich bin grad am lernen und zerbrech mir bei dieser Aufgabe schon seit Tagen den Kopf, also ich soll: eine echte Teilmenge U von R^3 angeben , so dass Uein Untervektorraum des R-Vektorraums R^3 ist
Ich bin so weit gekommen das ein Vektorraum drei dinge erfüllen muss um ein Untervektorraum zu sein -U darf nicht leer sein -für alle und - für alle
Aber ich weiß nicht wie ich das umsetzen muss könnte mir das jemand zeigen anhand eines Beispiels ist wirklich dringend, weil ich morgen meine Prüfung habe :(
|

|
 |
|
Kann mir da niemand helfen is wirklich wichtig :( |
 |
|
Doppelpost - siehe www.onlinemathe.de/forum/echte-Teilmenge-mit-bestimmten-Vektoren-bestimmen Ok, dreamerkid... eigentlich wollte ich ja nicht antworten; aber ich bin einfach ein lieber Kerl. Das Ziel ist es eine Menge zu finden, die die verlangten Bedingungen erfüllt. Wir fangen also klein an, tun ein paar Vektoren in unsere Menge und erweitern diese Menge so lange mit Vektoren aus bis die Bedingungen erfüllt sind. Wir benutzen die Bedingungen also um festzustellen welche Vektoren in die Menge hinein sollen. Aus der 3. Bedingung folgt direkt, dass in der Menge M sein muss. Denn: Sei irgend ein Vektor aus - so einen gibts, weil M ja laut der 1. Bedingung nicht leer sein darf. Nun wählen wir und erhalten: - und diese muss ja in M sein. Wir haben also bisher und tatsächlich ist dies schon ein Unterraum. Du kannst nun selbst überprüfen in dem du bildest u.s.w. Man nennt auch den trivialen Unterraum von Sagen wir nun, wir wollen unseren Raum erweitern, so dass z.b. sein muss. Wie wir oben schon gesehen haben, muss auch in M sein - wir haben also schon zwei Vektoren die sicher in unserem Unterraum sein müssen. Wir schauen uns nun wieder die Bedingung 3 an. Wählen wir irgend ein , so können wir mit den Vektor beliebig strecken - und auch dieser Vektor muss dann in sein. Es ist also so, dass jeder Vektor der Form in M sein muss. Wir haben jetzt also: Bemerke, dass für da schon dabei ist. Auch das ist nun ein Unterraum - sogar der kleinste der beinhaltet. Wir haben bisher noch keinen Gebrauch von der Bedingung 2 gemacht - dies, weil alle Vektoren die bisher aufgetreten sind linear abhänig waren. Wollen wir nun zusätzlich zu auch in unserem Vektorraum haben, dann stellen wir erst fest, dass wegen der Begründung wie oben auch alle Vektoren der Form in M sein müssen. Wir haben nun also: Doch Bedingung 2 zwingt uns dazu, dass wir auch alle linearkombinationen der Vektoren in unseren Vektorraum nehmen. Denn: muss ja auch in M sein. Wir bemerken auch, dass durch ersetzt werden kann, weil b ja eine Konstante ist, und wir die Konstante einfach doppelt so gross wählen können. Also erhalten wir: und alle diese Vektoren müssen nun in M sein. Also ist M: Dies ist nun der kleinste Raum der die zwei verlangten Vektoren beinhaltet. Wenn wir nun z.b. auch noch dazu holen wollen müssen wir nichts ändern, weil sich dieser Vektor schon durch ausdrücken lässt. Ich hoffe das macht die Sache für dich klarer, und bitte, antworte nicht schon nach 1 Minute und sage, dass du das nicht verstehst, sonst muss ich jemanden erwürgen. |
|
Diese Frage wurde automatisch geschlossen, da der Fragesteller kein Interesse mehr an der Frage gezeigt hat.
|
630254
630232









 gilt
gilt 
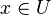 und
und 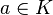 gilt
gilt 